জ্যোতির্বিজ্ঞান ১০১: লেকচার ০১.৪
কোপার্নিকাসের আগে
পিথাগোরাসের (খ্রিস্টপূর্ব/পূ ৫৭০-৪৯৫) শিষ্য ফিলোলাওস (পূ ৪৭০-৩৮৫) বলেছিলেন, আকাশের সবকিছুর মতো পৃথিবীও ঘুরছে, তবে সূর্যের চারদিকে নয়। পৃথিবী, চাঁদ, বুধ, শুক্র, সূর্য, মঙ্গল, বৃহস্পতি, শনি, নক্ষত্রসমষ্টি সবাই একটা অগ্নিপিণ্ডের চারদিকে ঘুরছে। সূর্য এই অগ্নিপিণ্ড থেকে আলো নিয়ে গ্রহদের মধ্যে বিতরণ করে।
প্লেটোর (পূ ৪২৮-৩৪৮) ছাত্র এওদক্সোস (Εὔδοξος–Eudoxus; পূ ৪০৮-৩৫৫) কে অনুসরণ করে এরিস্টটল (পূ ৩৮৪-৩২২) যে বিশ্বতাত্ত্বিক মডেল বানিয়েছিলেন তাতে পৃথিবী গোটা ব্রহ্মাণ্ডের কেন্দ্রে। পৃথিবীকে ঘিরে ৯টি বস্তু আছে। ভিতরের ৭টি হচ্ছে যথাক্রমে চাঁদ, বুধ, শুক্র, সূর্য, মঙ্গল, বৃহস্পতি ও শনি। ৮ম বস্তুটি হচ্ছে স্থির তারা/নক্ষত্র দের গোলক–তারাগোলক। আর সবার বাইরে আছে ‘প্রাইম মুভার’ (‘মহাচালক’) এর গোলক যা ৫৫টি গোলকের মাধ্যমে সবগুলো বস্তুকে নির্দিষ্ট নিয়মে ঘোরায়। তারাগোলকটিতে প্রোথিত তারাগুলো একে অপরের সাপেক্ষে কখনো স্থান পরিবর্তন করে না, কেবল পুরো গোলকটা ২৪ ঘণ্টায় একবার পৃথিবীকে আবর্তন করে। কিন্তু ভিতরের ৭টি বস্তু ২৪ ঘণ্টায় একবার আবর্তনের (আহ্নিক গতি) পাশাপাশি, তারাগোলকের তারাদের সাপেক্ষে একেক দিন একেক জায়গায় থাকে (বার্ষিক গতি)। তবে সব নক্ষত্রের কাছ দিয়ে তারা যায় না, কেবল নির্দিষ্ট ১২টি তারামণ্ডলের মধ্য দিয়ে যাতায়াত করে, যে তারামণ্ডলগুলোকেই রাশিচক্র বলে। এই ভ্রমণের কারণেই গ্রিকরা এই ৭টি বস্তুকে ‘ἀστὴρ πλανήτης’ (‘আস্তের প্লানেতিস’–‘ভ্রমনশীল নক্ষত্র’) ডাকত।
এওদক্সোস-এরিস্টটল-টলেমি কৃত বিশ্বমডেল:

এই মডেলের মহাসমস্যা ৪টি:
- পৃথিবীকে এক্কেবারে কেন্দ্রে রাখলে ঋতুর দৈর্ঘ্যের এবং ৭বস্তুর গতির হিসাব মেলে না।
- ৭বস্তুর মধ্যে চাঁদ-সূর্য ছাড়া বাকি ৫টি’র ‘প্রতীপ গতি’ আছে; অর্থাৎ তারা মাঝেমাঝে রাশিচক্রের মধ্য দিয়ে সম্মুখ-গমন (‘প্রগতি’) থামিয়ে উল্টো দিকে যেতে শুরু করে, এবং কিছুদিন পর আবার ‘প্রগতিশীল’ হয়।
- প্রতীপ গতির সময় ৫বস্তুর উজ্জ্বলতা বেড়ে যায়।
- প্রতীপ গতির সময় ৫বস্তুর বেগ বেড়ে যায়।
গ্রিক আয়োনিয়া’র সামোস দ্বীপের আরিস্তার্কোস (পূ ৩১০-২৩০) বলেছিলেন: সূর্য সবার কেন্দ্রে, পৃথিবী-চাঁদ সহ সব গ্রহ সূর্যের চারদিকে আবর্তনশীল, আর অন্য তারাগুলোও একেকটা সূর্য। তার হাইপোথিসিস ব্যবহার করে আর্কিমিডিস (পূ ২৮৭-২১২) “সাম্মিতিস” (Ψαμμίτης–The Sand Reckoner) নামক গবেষণাপত্রে গোটা মহাবিশ্বের আকার হিসাব করেন এবং মহাবিশ্বে মোট কতগুলো বালুকণা আঁটবে তা নির্ণয় করেন।
মেসোপটেমিয়া’র গ্রিক জ্যোতির্বিদ সেলেউকোস (Σέλευκος–Seleucus; পূ ১৯০-১৫০) আরিস্তার্কোসের মতবাদ সমর্থন করেন। কিন্তু বাস্তবিক কারণেই এই সৌরকেন্দ্রিক মডেল অন্য কারো কাছে গ্রহণযোগ্যতা পায়নি।
সবাই বরং উপরের ৪টি সমস্যা সমাধান করে ভূকেন্দ্রিক মডেলকেই সমর্থনের চেষ্টা করে। সমস্যাগুলো সমাধান করেছেন প্রধানত আপোলোনিওস (পূ ২৬২-১৯০), হিপ্পার্কোস (পূ ১৯০-১২০), এবং টলেমি (৯০-১৬৮)। টলেমি আগের সবার কাজ একত্রিত করে তার অতিবিখ্যাত “আলমাজেস্ট” (১৫০) বইয়ে একটা ‘ত্রুটিমুক্ত’ বিশ্বমডেল উপস্থাপন করেন।
এতে উপরের ৪টি সমস্যা সমাধানের চেষ্টা করা হয় এভাবে:
- পৃথিবীকে বিশ্বের কেন্দ্র থেকে একটু দূরে স্থাপন করা হয়। কিন্তু তারপরও পৃথিবীকে ‘কেন্দ্র’ বলা হতে থাকে এবং আসল কেন্দ্রটাকে বলা হয় ‘উৎকেন্দ্র’ (eccentric)। ৭বস্তু যে কক্ষপথে আবর্তন করে তার নাম ছিল ‘শীঘ্রবৃত্ত’ (deferent), যার কেন্দ্র পৃথিবী নয়, বরং ‘উৎকেন্দ্র’।
- ৫বস্তু অর্থাৎ ৫টি গ্রহকে ‘মন্দবৃত্ত’ (epicycle) নামে আরেকটা বৃত্তের উপর স্থাপন করা হয়; প্রত্যেক গ্রহের মন্দবৃত্তের কেন্দ্র তার শীঘ্রবৃত্তের উপর; গ্রহটা মন্দবৃত্তের কেন্দ্রের চারদিকে ঘোরে, আর মন্দবৃত্তটা নিজে শীঘ্রবৃত্ত ধরে পৃথিবীর চারদিকে ঘোরে। মন্দবৃত্তে ঘোরার কারণেই গ্রহগুলোকে কখনো কখনো পৃথিবীর সাপেক্ষে উল্টোদিকে যেতে দেখা যায় যা হলো প্রতীপ গতির ব্যাখ্যা।
- প্রতীপ গতির সময় গ্রহ মন্দবৃত্তের ভিতরের দিকে অর্থাৎ পৃথিবীর কাছে থাকে, যে কারণে তাকে বেশি উজ্জ্বল দেখায়।
- উৎকেন্দ্র থেকে পৃথিবী যেদিকে তার ঠিক উল্টো দিকে ‘ইকুয়েন্ট’ (‘সমকারক’) নামে আরেকটা বিন্দু কল্পনা করা হয় যে বিন্দুর সাপেক্ষে গ্রহগুলোর বেগ একেবারে সুষম। ইকুয়েন্টের সাপেক্ষে বেগ সুষম থাকতে হলে, পৃথিবীর সাপেক্ষে গ্রহদের বেগ কখনো কম কখনো বেশি হতে হয়–এই হলো বেগবৃদ্ধির ব্যাখ্যা।
একসেন্ট্রিক (উৎকেন্দ্র), ডেফারেন্ট (শীঘ্রবৃত্ত), এপিসাইকেল (মন্দবৃত্ত) এবং ইকুয়েন্ট এর রেখাচিত্র:

কিন্তু তারপরও টলেমি’র মডেলে অনেক সমস্যা রয়ে যায়:
- মহাভজঘট। এ এক অবাস্তব মডেল, দেখেই বুঝা যাচ্ছে এটা গাণিতিক খেলা, প্রাকৃতিকভাবে এত জটিল গতিকাঠামো তৈরি হতে পারে না।
- প্লেটো-এরিস্টটল যে সুষম বৃত্তীয় গতির পৃষ্ঠপোষকতা করতেন তা রক্ষা করতে গিয়ে ইকুয়েন্ট এর মতো একটা কাল্পনিক বিন্দু প্রণয়ন করতে হচ্ছে।
- এতকিছু দিয়েও গ্রহদের গতি পুরোপুরি হিসাব করা যায় না। একেক গ্রহের জন্য ইচ্ছামতো একেক ব্যাসার্ধ্যের এপিসাইকেল; উৎকেন্দ্র থেকে পৃথিবী ও ইকুয়েন্টের একেক রকমের দূরত্ব ধরে নিতে হয়। গ্রহের অবস্থান নির্ণয়ের পদ্ধতি যত সূক্ষ্ণ হতে থাকে টলেমির মডেলের বিভিন্ন রাশি ততই বেশি ইচ্ছামাফিক পরিবর্তন করতে হয়।
ভারতে আর্যভট্ট (৪৭৬-) বলেন পৃথিবী নিজ অক্ষের সাপেক্ষে ঘুরছে, কিন্তু ব্রহ্মগুপ্ত (৫৯৮-৬৭০) তার বিরোধিতা করেন।
১০০০ সালে ইবনুল হাইসাম (৯৬৫-১০৪০) টলেমি’র ইকুয়েন্ট বিন্দুর সমালোচনা করেন।
ইরানের মারাগাহ মানমন্দিরে নাসির আল-দিন আল-তুসি (১২০১-৭৪) “তুসি যুগল” দিয়ে ইকুয়েন্ট এর প্রয়োজনীয়তা দূর করেন।
সিরিয়ার দামেস্কে ইবনুল শাতির (১৩০৪-৭৫) প্রত্যেক গ্রহের জন্য ২টি মন্দবৃত্ত দিয়ে ইকুয়েন্ট দূর করেন।
ভারতে “কেরলীয় গণিত সম্প্রদায়” এর নীলকণ্ঠ সোম্যাজি (১৪৪৪-১৫৪৪) আর্যভট্টের ভাষ্য রচনা করতে গিয়ে একটা ভূসৌর-কেন্দ্রিক হাইপোথিসিস দেন: গ্রহগুলো সূর্যকে প্রদক্ষিণ করছে, যে সূর্য আবার পৃথিবীকে প্রদক্ষিণ করছে।
কোপার্নিকাসের বৈপ্লবিক হাইপোথিসিস
৪টি সমস্যা সমাধানের জন্য ৪টি ‘চতুর-কৌশল’ এবং তারপরও রয়ে যাওয়া ৩টি মহাফাঁক–এই সব দেখেই পোলীয়-জার্মান পাদ্রি-চিকিৎসক-জ্যোতির্বিদ নিকোলাস কোপার্নিকাস (১৪৭৩-১৫৪৩) টলেমিকে মেনে নিতে পারেননি।
তিনি তার অতিবিখ্যাত এবং একমাত্র বই De revolutionibus orbium coelestium (১৫৪৩) এ একটি বিকল্প মডেল প্রস্তাব করেন, অনেকটা আরিস্তার্কোসের মতোই। সূর্য সবার কেন্দ্রে, তাকে কেন্দ্র করে সবাই সুষম বৃত্তীয় বেগে ঘুরছে, অন্য তারাগুলো বহু দূরে। সূর্য থেকে দূরত্বের দিক দিয়ে বস্তুগুলোর ক্রম হচ্ছে: বুধ, শুক্র, পৃথিবী-চাঁদ, মঙ্গল, বৃহস্পতি, শনি, তারাগোলক।
কোপার্নিকাস নিজে মহাবিশ্বের যেই ছবিটি এঁকেছিলেন:
এই মডেল দিয়ে ৪টি সমস্যার সমাধান করা হয় এইভাবে:
- সূর্যকে কেন্দ্রে বসালে কোনো উৎকেন্দ্র ছাড়াই ঋতুর দৈর্ঘ্য, গ্রহদের গতি ব্যাখ্যা করা যায়। তবে এটা পুরোপুরি ব্যাখ্যা করতে ইয়োহানেস কেপলার (১৫৭১-১৬৩০) আসা পর্যন্ত অপেক্ষা করতে হবে।
- পৃথিবীকে সূর্যের চারদিকে ঘোরাতে শুরু করলে প্রতীপ গতি ব্যাখ্যা কোনো ব্যাপারই না। ধরুন একটা বাসে যাচ্ছেন যার বেগ ঘণ্টায় ৬০ কিমি, এমন সময় পাশে আরেকটা বাস চলে এল যার বেগও ৬০ কিমি/ঘণ্টা। এখন আপনার বাসের চালক বেগ বাড়িয়ে ৮০ কিমি/ঘণ্টায় যদি পাশের বাসকে ছেড়ে এগিয়ে যায় তাহলে পাশের বাসের দিকে তাকালে দেখবেন যে, সেটি পিছনের দিকে চলে যাচ্ছে। একইভাবে, সূর্য প্রদক্ষিণকালে যখন পৃথিবী কোনো গ্রহকে ছাড়িয়ে চলে যায় তখন সেই গ্রহকে পিছনে যেতে দেখা যায়, যা হলো প্রতীপ গতি।
- প্রতীপ গতি তখনই হবে যখন পৃথিবী আর অন্য গ্রহটি একই দিকে যাচ্ছে, ঠিক যেমন আগের উদাহরণ কাজ করতে হলে বাস দুটিকে একই দিকে যেতে হবে। আর পৃথিবী ও অন্য গ্রহ একই দিকে গতিশীল থাকার অর্থই হচ্ছে তারা পরস্পরের অপেক্ষাকৃত কাছাকাছি আছে। তাই প্রতীপ গতির সময় গ্রহের উজ্জ্বলতা বাড়ে।
- গতি বেশি দেখার কারণ হচ্ছে কৌণিক বেগের মৌলিক প্রকৃতি। কাছ দিকে যাওয়া একটা পাখিকে দূর দিয়ে যাওয়া একটা বিমানের চেয়ে বেশি বেগবান মনে হয়। প্রতীপ গতির সময় যেহেতু গ্রহটা আগের চেয়ে পৃথিবীর অনেক কাছে থাকে সেহেতু তার বেগও বেশি মনে হয়।
কোপার্নিকাস তো ৪ সমস্যা সমাধানে পুরো উৎরে গেলেন। কিন্তু, এগুলো তো টলেমি’র মডেলও ব্যাখ্যা করতে পারত। টলেমি’র মডেলে যে ৩টি সমস্যা রয়েই গিয়েছিল সেগুলো নিয়ে দেখা যাক কোপার্নিকাস কী বলেন।
- সৌরকেন্দ্রিক মডেলে অন্তত গতিবিদ্যার দিক দিয়ে কোনো ভজঘট নেই; এবং এটা বাস্তবে খুবই সম্ভব। এবং টলেমি’র তুলনায় এটা অনেক অনেক বেশি সরল, সুন্দর, প্রাকৃতিক ও নান্দনিক।
- সুষম বৃত্তীয় গতি এবারে পুরোপুরি প্রতিষ্ঠিত হয়েছে। এই মডেলে অন্য কোনো গতি নেই। আমরা এখন জানি যে, সুষম বৃত্তীয় গতির ধারণার কোনো ভিত্তি নেই। কিন্তু সে সময় সুষমগতিটা অনেক বড় ব্যাপার ছিল, তাই তখনকার প্রেক্ষাপটে একে কোপার্নিকাসের সফলতাই বলতে হবে।
- এইখানে যে তখন কোপার্নিকাস টলেমির চেয়ে বেশি সঠিক ছিল তা বলা যাবে না। এমনকি কিছু ক্ষেত্রে টলেমির মডেলই বেশি ভালো ফল দিত। কোপার্নিকাসের ধারণাটা ঠিক হলেও কক্ষপথের আসল আকৃতি জানা না থাকার কারণে, হিসাবে তার মডেল কিছু ভুল দেখাতে বাধ্য।
কোপার্নিকাস আগের ৪+৩=৭ সমস্যার ৬ টিতে পুরোপুরি সফল, ১টিতে আংশিক সফল; যেখানে টলেমি কেবল ৪টিতে সফল ছিলেন।
আসলে ৩সমস্যার ২নং টি অপসারণ করলে, অর্থাৎ সুষম বৃত্তীয় গতির ধারণা ত্যাগ করলে, এখানের ৩নং সমস্যারও সমাধান হয়ে যায়। এবং পাশাপাশি ৪সমস্যার ১ম টিরও সমাধান হয়ে যায়। কেপলার এটাই করেছিলেন। তার মানে কেপলারের পর এই ৭সমস্যার সবগুলোই দূরীভূত হয়েছিল।
এর মধ্যে গালিলেও এসে কোপার্নিকাসের দল ভারী করেছিলেন অন্যভাবে। তিনি উল্টো পথে হাঁটেন: ভূকেন্দ্রিক মডেলের নতুন আরো ৩টা সমস্যা বের করেন:
- শুক্রগ্রহের সবগুলো কলা আছে, অর্থাৎ চাঁদের মতোই শুক্রগ্রহের পূর্ণিমা, অমাবস্যা, হেলাল (crescent), অর্ধাধিক (gibbous) ইত্যাদি সব দশা দেখা যায়; কারণ পৃথিবী থেকে একেক সময় শুক্রের একেক অংশ সূর্যালোকিত দেখা যায়। ভূকেন্দ্রিক মডেল সত্য হলে শুক্রের হয় কেবল অমাবস্যা-হেলাল নয় কেবল পূর্ণিমা-অর্ধাধিক কলা দেখা যেত; দুটো কলাই দেখতে পাওয়া সম্ভব কেবল যদি পৃথিবী ও শুক্র দুটোই সূর্যকে প্রদক্ষিণ করে এবং যদি শুক্রের কক্ষপথ সূর্যের অপেক্ষাকৃত কাছে হয়।
- সৌরকলঙ্ক স্থান পরিবর্তন করে। এটা ভূসৌরকেন্দ্রিক মডেল দিয়ে মোটামুটি ব্যাখ্যা করা যায়, তাও অনেক জটিলভাবে।
- বৃহস্পতির উপগ্রহ আছে।
কিন্তু ধীরে… কোপার্নিকাস আবার নতুন এমন কোনো সমস্যা তৈরি করে ফেললেন না তো, যেগুলো টলেমির মডেলে ছিল না? হ্যাঁ, সেই সময়কার প্রেক্ষাপটে কোপার্নিকাস নতুন কিছু সমস্যায় আসলেই পড়েছিলেন:
- সবাই ভাবত, আকাশের সবকিছু অতিহালকা ও অজানা কোনো পদার্থ (‘quintessence’; অদৃশ্য পদার্থ–dark matter–এর সাথে সাদৃশ্য পাচ্ছেন কী?) দিয়ে তৈরি বলে শূন্যে ভেসে বেড়াতে পারে, কিন্তু পৃথিবী যেহেতু অতিভারী সেহেতু তাকে ঘোরানের সাধ্যি কারো নেই। তো পৃথিবী ঘুরছে কী করে?
- পৃথিবী যদি আসলে ঘূর্ণনশীল হয়ে থাকে, তবে আমরা তার প্রভাব টের পাচ্ছি না কেন? আমরা ছিটকে পড়ে যাচ্ছি না কেন?
- তখনকার সব বিদ্যার ভিত্তি ছিল এরিস্টটলের পদার্থবিদ্যা, যা পৃথিবীর অনড়তার উপর ভিত্তি করে প্রতিষ্ঠিত, এবং যা দিয়ে অনেক অনেক ঘটনা অনেকযুগ ধরে সবাই ব্যাখ্যা করে আসছে। ঘুরন্ত পৃথিবীতে এই পদার্থবিদ্যা কাজ করবে না, কিন্তু বিকল্প কোনো পদার্থবিদ্যা তো নেই। এখন? (উল্লেখ্য, গালিলেও সেই বিকল্প দেবেন ভবিষ্যতে।)
- পৃথিবী যদি সূর্য প্রদক্ষিণ করে তবে ‘লম্বন’ (parallax) ক্রিয়ার কারণে নক্ষত্রদের অবস্থান সময়ের সাথে সাথে পাল্টানো উচিত। অপেক্ষাকৃত কাছের একটি তারাকে আমরা দূরের তারাদের পটভূমির সাপেক্ষে দেখি। আমাদের অবস্থান থেকে তারা পর্যন্ত একটা রেখা টেনে সেটাকে পিছনে তারাদের পটভূমি পর্যন্ত বর্ধিত করলে রেখাটা গিয়ে পটভূমির যেই বিন্দুতে ছেদ করবে কাছের তারাকে আমরা সেইখানেই দেখব। এখন যদি দুইটা ভিন্ন জায়গা থেকে দেখি, তাহলে দৃষ্টিরেখা দুটি পটভূমির দুইটা ভিন্ন বিন্দুতে ছেদ করবে। তার মানে কাছের একই তারাকে আমরা পৃথিবীর কক্ষপথের একেক জায়গা থেকে একেক জায়গায় দেখব। নিচের ছবিতে ব্যাপারটা দেখানো হয়েছে।
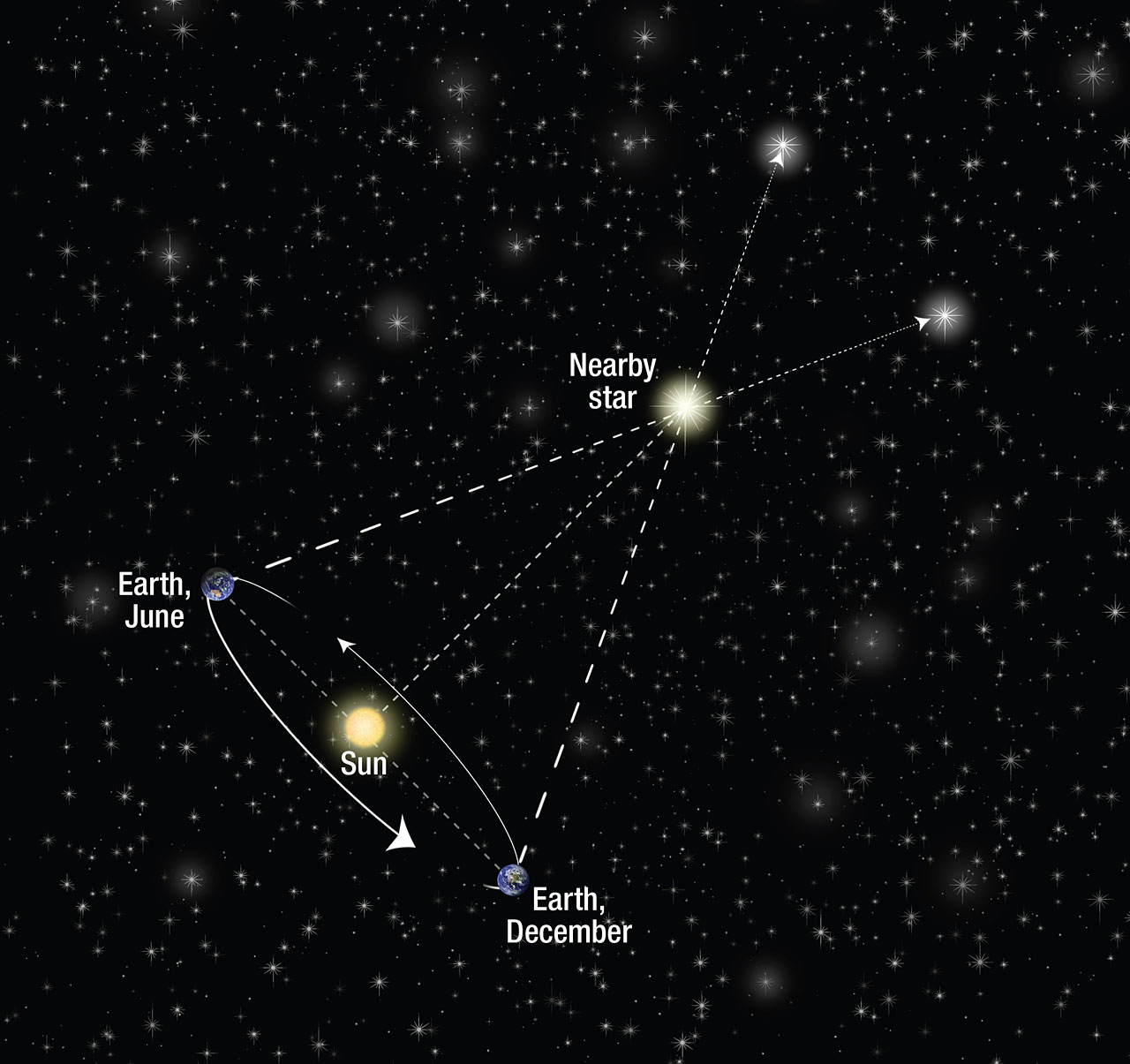
নতুন আরো ৪টি সমস্যা তৈরি হলো। গালিলেও, নিউটন এসে নতুন পদার্থবিদ্যা তৈরি করেন। আর ১৮৩৭ সালে প্রথম তারার লম্বন পরিমাপ করা হয়।
শেষটুকু জানতে ভিডিওটি দেখুন।



