ভূমিকা
পরিসংখ্যানের জটিলতম এবং সবচেয়ে রহস্যময় বিষয়টির নাম হাইপোথিসি টেস্টিং। কিন্তু ব্যাপারটাকে আমি এমনভাবে শেখানোর চেষ্টা করবো যে এই পাতাটি পড়ার পরে আপনি বলতে বাধ্য হবেন—‘এত্ত সহজ জিনিস!’ অন্তত কনসেপ্টটা বুঝতে পারবেন এটুকু র নিশ্চয়তা দিচ্ছি। বাকীটুকু বোঝার জন্য আগের লেকচারগুলোর উপর অনেকাংশে নির্ভর করতে হবে।
হাইপোথিসিস টেস্টিংকে বাংলায় বলব প্রকল্প যাচাই। আমাদের একটি হাইপোথিসিস থাকবে যেটাকে আমরা পরিসংখ্যানিকভাবে যাচাই করে দেখব সেটি ঠিক না বেঠিক।
হাইপোথিসিস কী তা আমি এখনই বলবনা। আগে একটা উদাহরণ দেখি।
উদাহরণ ১ (আমার হাতে বই)
কল্পণা করুন আমার হাতে কাগজের একটি পাতা রয়েছে। একটি মাত্র শীট। আমি এই একপাতা কাগজ হাতে নিয়ে দাবী করছি এটি একটি বই। আপনি প্রমাণ করতে পারবেন যে এটি বই না?
আমি নিশ্চিত আপনারা সবাই বেশ কয়েকটি শক্ত যুক্তি দাঁড় করিয়ে খুব সহজেই প্রমাণ করতে পারবেন যে এটি বই নয়। কিন্তু তার পরেও কি নিশ্চিত হওয়া যাবে যে এটি বই নয়? এমনতো হতে পারে আমি এক পাতার একটি বই ছাপিয়েছি। হতে পারে না? পারে। তার মানে যা দাঁড়ালো—আপনি ১০০ভাগ নিশ্চিত না হলেও এমন কতগুলো প্রমাণ উপস্থাপন করতে সক্ষম হবেন যাতে প্রায় নিশ্চিতভাবেই বলা যায় এটি বই নয়।
এটি যে বই নয় তার পক্ষে যুক্তিগুলো এরকম—
১) এখানে মাত্র একটি পাতা রয়েছে
২) দেখতে বইয়ের মতো নয়
৩) কাভার অনুপস্থিত
এরকম অনেক যুক্তি দেয়া যাবে। লক্ষ্যণীয় যে আপনারা আমার দাবীর বিপক্ষে যুক্তি দাঁড় করাচ্ছেন। আপনারা প্রমাণ করতে চাইছেন আমার দাবীটি সঠিক নয়।
কেউ হয়তো ভাবছেন দাবীর পক্ষেও তো যুক্তি দেয়া যেতে পারে। হ্যাঁ পারে, কিন্তু চেষ্টা করে দেখুন যুক্তিগুলো তেমন যুতসই হবে না। কারণ দাবীর পক্ষের যুক্তিগুলো বাস্তবিক নয়।
উপরের যুক্তিগুলোর নীরিখে আমরা কতগুলো “টেস্ট” বা “যাচাই পদ্ধতি”-র কথা চিন্তা করতে পারি। টেস্ট মানে কতগুলো প্রশ্নের সমাহার (যেমন পরীক্ষার প্রশ্নপত্র), আবার টেস্ট মানে যাচাই (যেমন ব্লাড টেস্ট করে ডেঙ্গুর জীবানু আছে কিনা তা যাচই করা). তেমনি আমার দাবীকে উপরের তিনটি প্রশ্ন দিয়ে বাতিল করার জন্য দরকার টেস্ট। উপরের তিনটি যুক্তির পরিপ্রেক্ষিতে টেস্ট গুলো এরকম হতে পারে –
১) বইটির পাতার সংখ্যা দিয়ে যাচাই করা
২) বইটি দেখতে কেমন সেটা দিয়ে যাচাই করা (বইয়ের মতো কিনা)
৩) বইটির কাভার দিয়ে যাচাই করা (কাভার আছে না নাই)
তাহলে উপরে দাবীর সাথে সংশ্লিষ্ট এরকম তিনটি অংশ আমরা দেখতে পাই—
প্রথমত: দাবী
দ্বিতীয়ত: দাবী যাচাই করার পদ্ধতি (টেস্ট বা যাচাই প্রকৃয়া)
তৃতীয়ত: দাবীর বিপক্ষে যুক্তিসমূহ, যার ভিত্তিতে দাবীটিকে বাতিল করে দেয়া যাবে অথবা বাতিল করা যাবে না।
আমি কিন্তু এরই মধ্যে প্রকল্প যাচাইয়ের বিষয়টি পড়িয়ে ফেলেছি।
ভাবছেন, সেটা কিভাবে সম্ভব?
আসলেই পড়িয়ে ফেলেছি। ব্যাপারটা আসলে এরকমই। আসুন উপরের উদাহরণটিকে একটু ব্যাখ্যা করি।
দাবী (Hypothesis)
এখানে দাবীটি ছিল হাতে ধরা কাগজের পাতাটি একটি বই। এটিই আমাদের হাইপোথিসিস। প্রকৃতপক্ষে হাইপোথিসিস বা প্রকল্প হল জনগোষ্ঠির কোন বৈশিষ্ট্য সম্পর্কে একটি কল্পনা বা দাবী। যেমন, একটি দাবী হতে পারে এরকম– এই কোর্সে অংশগ্রহণকারী শিক্ষার্থীদের ১০ শতাংশের কম শিক্ষার্থী নতুন লেকচার প্রকাশিত হলে সেটা পড়ে দেখে। এখানে জনগোষ্ঠি হল এই কোর্সে অংশ নেয়া সকল শিক্ষার্থীবৃন্দ। আর সকল শিক্ষার্থীদের কত শতাংশ নতুন লেকচার প্রকাশিত হলে সেটা পড়ে দেখে সেটি হলো এই জনগোষ্ঠির একটি বৈশিষ্ট্য বা পরামান (parameter) . আমাদের দাবীটি এই পরামান সম্পর্কে।
এরকম দাবীকে পরিসংখ্যানের ভাষায় বলে নাস্তি প্রকল্প বা null hypothesis. এরকম একটি প্রকল্পকে যদি আমরা যাচাই করার পর বাতিল করে দেই তাহলে আমরা কী সিদ্ধান্ত নেব? সিদ্ধান্ত গ্রহণে সুবিধার জন্য আমাদের বিকল্প একটি দাবীও মাথায় রাখতে হয়। বিকল্প দাবীটি হয় মূল দাবীর পুরোপুরি উল্টো। আমাদের মূল দাবী যদি হয় “কাগজটি একটি বই”, তাহলে বিকল্প দাবীটি হবে “এটি বই নয়”. দাবী দুটিকে আমরা এভাবে লিখি–
নাস্তি-প্রকল্প (Null Hypothesis) : কাগজটি একটি বই
প্রতি-প্রকল্প (Alternative Hypothesis): কাগজটি বই নয়
যাচাই সূত্র (Test Statistic)
দ্বিতীয় অংশে আছে দাবী যাচাই করার পদ্ধতি। এটি এমন একটি নিয়ম বা সূত্র যার ভিত্তিতে কিছু শর্তকে ব্যবহার করে দাবীটির সত্যতার সম্ভাব্যতা (Possibility of being correct) যাচাই করা হয়।
উপরে আমরা তিনটি যাচাই পদ্ধতির কথা বলেছি।
১) বইটির পাতার সংখ্যা দিয়ে যাচাই করা
২) বইটি দেখতে কেমন সেটা দিয়ে যাচাই করা (বইয়ের মতো কিনা)
৩) বইটির কাভার দিয়ে যাচাই করা (কাভার আছে না নাই)
ধরা যাক আমাদের উদাহরণের জন্য প্রথম পদ্ধতিটিই সবচেয়ে গ্রহণযোগ্য। বাকী গুলো দিয়েও কাজ হবে কিন্তু আমরা প্রথমটিকেই ব্যবহার করব। এ থেকে বুঝতে পারছি একটি দাবী যাচাই করার জন্য অনেক ধরনের যাচাই পদ্ধতি থাকতে পারে।
পরিসংখ্যানের ভাষায় যাচাই করার এই পদ্ধতিকে বলে টেস্ট স্ট্যাটিসটিক (Test Statistic). টেস্ট স্ট্যাটিসটিক এমন একটি সূত্র বা নিয়ম যার বৈশিষ্ট্য আমাদের আগে থেকেই জানা থাকে। যেমন এই উদাহরণে বইয়ের পাতার সংখ্যা বলতে আমরা বুঝতে পারছি বইটিতে কতটি পাতা আছে, এবং পাতা বলতে আমরা কী বুঝি সব কিছুই আমাদের জানা। এখানে অজানা বা অসম্পূর্ণ কিছুই নেই। অন্যভাবে, টেস্ট স্ট্যাটিসটিককে মাপকাঠি বলা যেতে পারে। মাপকাঠি দিয়ে যেমন আমরা মেপে বলতে পারি একজন মানুষের উচ্চতা ৫ ফুট নাকি ৫ ফুটের কম, তেমনি পাতার সংখ্যা দিয়ে আমরা বলতে পারবো এটি বই নাকি বই নয়।
সিদ্ধান্ত নীতি (Decision Rule)
যাচাই পদ্ধতি ঠিক করার পর এর ভিত্তিতে সিদ্ধান্ত নেয়ার জন্য আমাদের একটি নিয়ম স্হাপন করতে হবে। পাতার সংখ্যা যদি আমাদের টেস্ট স্ট্যাটিসটিক হয় তাহলে কত পাতার কম হলে আমরা দাবীটি বাতিল করে দিব বা কত পাতার বেশী হলে দাবীটিকে বাতিল করতে পারবো না সেটিই আমাদের সিদ্ধান্ত নীতি বা decision rule.
যদি সিদ্ধান্ত নীতিটি হয় এমন যে পাতার সংখ্যা ৮ এর কম হলে আমরা একে বই বলতে পারবোনা, তাহলে বইটির পাতা গুনে (যেটি আমাদের যাচাই পদ্ধতি) যদি দেখি পাতার সংখ্যা ৮ এর কম তাহলে আমরা দাবীটিকে বাতিল করে দিব।
কত পাতার কম হলে আমরা দাবীটি বাতিল করে দিব সেটি পুরোটাই আমাদের ইচ্ছের উপর নির্ভর করছে। আমরা ১৬ পাতাকে কাটঅফ পয়েন্ট ধরতে পারি বা এরচে বড় সংখ্যাকেও ধরতে পারি আবার এরচে কম সংখ্যাকেও ধরতে পারি।
উদাহরণ ১ এর সমাধান
এবারে উদাহরণ ১ এর সমাধান করা যাক।
দাবী
নাস্তি-প্রকল্প: এটি একটি বই
প্রতি-প্রকল্প: এটি একটি বই নয়
যাচাই পদ্ধতি / টেস্ট স্ট্যাটিসটিক
বইয়ের পাতার সংখ্যা
সিদ্ধান্ত নীতি
বই হতে হলে পাতার সংখ্যা কমপক্ষে ৮ হতে হবে। অর্থাৎ পাতার সংখ্যা ৮এর কম হলে এটি বই নয়।
টেস্ট স্ট্যাটিসটিকের মান
আমরা গুনে দেখলাম বই বলে যেটিকে দাবী করা হচ্ছে তার পাতার সংখ্যা ১টি।
সিদ্ধান্ত
আমরা দেখলাম যেহেতু টেস্ট স্ট্যাটিসটিকের মান ৮ এর কম, সেহেতু আমরা বলবো নাস্তি প্রকল্পটির বিরুদ্ধে যথেস্ট প্রমাণ আছে। অর্থাৎ আমাদের সিদ্ধান্ত নীতি অনুসারে দাবীটির বিরুদ্ধে প্রমাণ পাওয়া গিয়েছে। দাবীটি যদি সত্যি হতো তাহলে পাতার সংখ্যা কমপক্ষে ৮ হতে হতো। যেহেতু পাতার সংখ্যা ৮ এর কম, তাই দাবীটিকে আমরা বাতিল করার পক্ষে মত দিলাম এবং বললাম দাবীটির বিরুদ্ধে যথেষ্ট প্রমাণ আছে।
সাবধানতা (Caution)
নাস্তি প্রকল্প বাতিল করেছি বলেই প্রতিপ্রকল্পটি গ্রহণ করবো ব্যাপারটা এমন নয়। আমরা এটাও বলতে পারবোনা যে নাস্তি প্রকল্পটি ভুল। আমরা বলতে পারবো নাস্তি প্রকল্পের বিরুদ্ধে যথেষ্ট প্রমাণ পাওয়া গিয়েছে । অন্যভাবে বলা যাবে, প্রতিপ্রকল্পের পক্ষে প্রমাণ পাওয়া গিয়েছে (যে এটি বই নয়). আমরা কখনোই প্রকল্পকে গ্রহণ বা বাতিল করতে পারবো না। আমরা শুধু প্রকল্প গ্রহণ করা বা বাতিল করার পক্ষে প্রমাণ হাজির করতে সক্ষম। গভীরভাবে চিন্তা করলে দেখবেন এটাই বাস্তবসম্মত।
জনগোষ্ঠির গড় নিয়ে দাবী যাচাই (Hypothesis test for population mean)
ধরি আমাদের হাইপোথিসিস বা দাবীটি এরকম: শিক্ষক ডট কমে যারা সাইন-আপ করেছেন তাদের গড় বয়স ২৪ বছর। এটি আমাদের নাস্তি প্রকল্প। এটিকে আমরা যাচাই করতে চাই। যাচাই করার জন্য আমাদের একটি প্রতিপ্রকল্প ধরতে হবে। সেটি তিনভাবে ধরতে পারি—
ক) যারা সাইন-আপ করেছে তাদের গড় বয়স ২৪ এর কম, অথবা
খ) যারা সাইন-আপ করেছে তাদের গড় বয়স ২৪ এর বেশী, অথবা
গ) যারা সাইন-আপ করেছে তাদের গড় বয়স ২৪ নয়
এখন আমাদের দরকার একটি যাচাই পদ্ধতি বা টেস্ট স্ট্যাটিসটিক যার মানের উপর ভিত্তি করে আমরা প্রকল্পটি যাচাই করবো। এই টেস্ট স্ট্যাটিসটিক হতে হবে এমন একটা কিছু যার বৈশিষ্ট্য আমরা ভালোভাবে জানি। চিন্তা করুন তো কী হতে পারে সেটি?
উত্তরটা আন্দাজ করতে পারছেন না হয়তো। তাহলে বরং দেখি কিভাবে আমরা এই দাবী যাচাই করতে পারি। একটা পদ্ধতি হতে পারে এই জনগোষ্ঠি থেকে কিছু সংখ্যক নমুনা নিয়ে সেখানে থেকে গড় বের করা। তারপর সেই গড়কে নাস্তি কল্পনায় যে গড় ধরা হয়েছে (২৪ বছর) তার সাথে তুলনা করে একটা সিদ্ধান্ত নেয়া। ধরি, আমরা ৫০ জন শিক্ষার্থীকে দৈব চয়নের মাধ্যমে নির্বাচিত করলাম এবং তাদের গড় বয়স পাওয়া গেল ২৭। এখন আপনি কী সিদ্ধান্ত নিবেন? দাবীটিকে বাতিল করবেন নাকি করবেন না?
মনে মনে হয়তো ভাবছেন নমুনা গড় যেহেতু ২৪ এর বেশী তাই দাবীটিকে বাতিল করা যায় না। আপনার ভাবনা ঠিকই আছে, কিন্তু ভেবে দেখুন নমুনা গড় যদি ৩৫ বছর হতো তাহলে কী করতেন? নিশ্চয়ই বলতেন না যে অংশগ্রহণকারী শিক্ষার্থীদের গড় বয়স ২৪।
আবার ধরুন নমুনা থেকে গড় বয়স পেলেন ২২. তখন আপনি বলতে পারেন, ২২ সংখ্যাটি দাবীকৃত বয়স, ২৪, এর বেশ কাছে। সে হিসেবে দাবীটি হয়তো ঠিক আছে। কিন্তু ধরুন নমুনা গড় যদি হতো ১৮ তাহলে কি দাবীর পক্ষে সিদ্ধান্ত নিতেন? সম্ভবত নিতেন না।
তাহলে আমরা দেখতে পাচ্ছি সিদ্ধান্ত গ্রহণের সাথে সিদ্ধান্ত নীতির সম্পর্ক রয়েছে। আর সিদ্ধান্ত নীতির কাটঅফ (উদা. ২২এর কম কিংবা ২৬ এর বেশী) নির্ভর করবে প্রতি-প্রকল্পের উপর।
যদি প্রতিপ্রকল্প হয় ক) গড় বয়স ২৪ এর কম, তাহলে আপনার কাটঅফ হতে পারে ২২ অর্থাৎ নমুনা গড় ২২ এর কম হলে আপনি দাবী বাতিল করবেন। অর্থাৎ প্রাপ্ত নমুনা গড় ২২ এর কম হলে দাবিটি বাতিল হবে।
আর যদি প্রতিপ্রকল্প হয় খ) গড় বয়স ২৬ এর বেশী, তাহলে কাটঅফ পয়েন্ট হতে পারে ২৬ বছর। অর্থাৎ প্রাপ্ত নমুনা গড় ২৬ এর বেশী হলে দাবিটি বাতিল হবে।
আর যদি প্রতিপ্রকল্প হয় গ) গড় বয়স ২৪ নয়, তাহলে আমাদের দুটি সংখ্যার সাথে তুলনা করতে হবে। এক্ষেত্রে কাটঅফ পয়েন্ট হতে পারে ‘২২এর কম অথবা ২৬এর বেশী।’
যাচাই সূত্র (Test Statistic)
জনগোষ্ঠি গড়ের উপর প্রকল্প যাচাই কিভাবে আমরা করতে পারি তা কিছুটা ধারণা করতে পারছি। আমরা সিদ্ধান্ত নিয়েছি যে নমুনা থেকে প্রাপ্ত গড় বয়স ২২এর কম হলে কিংবা ২৬ এর বেশী হলে আমরা দাবিটি বাতিল করতে পারবো। কিন্তু এই ২২ এবং ২৬ সংখ্যা দুটো কিভাবে নির্ধারণ করবো?
পরিসংখ্যানবিদগন টেস্ট স্ট্যাটিসটিক নির্ধারণ করার জন্য নমুনা বিন্যাসের (Sampling distribution) ধারণা প্রয়োগ করেন, এবং কাটঅফ পয়েন্ট বের করার জন্য সম্ভাবনার কনসেপ্ট ব্যবহার করেন। ধরা যাক জনগোষ্ঠিতে বয়সের ভেদ ১৬ অর্থাৎ বয়সের পরিমিত ব্যবধান ৪. তাহলে নমুনা গড়ের সম্ভাবনা বিন্যাস থেকে আমরা জানি
আমরা আরো জানি, সম্ভাবনা বিন্যাস জানা থাকলে কোন চলককে স্ট্যান্ডারডাইজ করে তার জেড স্কোর বের করা যায় —
এই জেড-স্কোরের সূত্রটিকেই আমরা টেস্ট স্ট্যাটিসটিক হিসেবে ব্যবহার করতে পারি। এর কারণ হল জেড স্কোরের সূত্রটিতে জনগোষ্ঠি গড় (মিউ) ছাড়া বাকী সবকিছুই আমাদের জানা আছে। আর মিউ এর স্হলে যদি আমরা মিউ এর হাইপোথেটিক্যাল মান—যেটি আমাদের নাস্তি প্রকল্প—বসাই তাহলে আমরা বলতে পারবো নাস্তি প্রকল্পটি সঠিক হলে টেস্ট স্ট্যাটিসটিকটি স্ট্যান্ডার্ড নরমাল বিন্যাস অনুসরণ করবে। অর্থাৎ নাস্তি প্রকল্পটি সঠিক হলে এর বিন্যাস হবে নরমাল যার গড় শুন্য এবং ভেদ বা পরিমিত ব্যবধান ১।
সিদ্ধান্ত নীতি
টেস্ট স্ট্যাটিসটিক নির্ধারণ করা হয়ে গেলে আমাদের কাটঅফ পয়েন্ট নির্ধারণ করতে হবে। কাজটি কঠিন নয় কেননা টেস্ট স্ট্যাটিসটিকটির সম্ভাবনা বিন্যাস নরমাল।
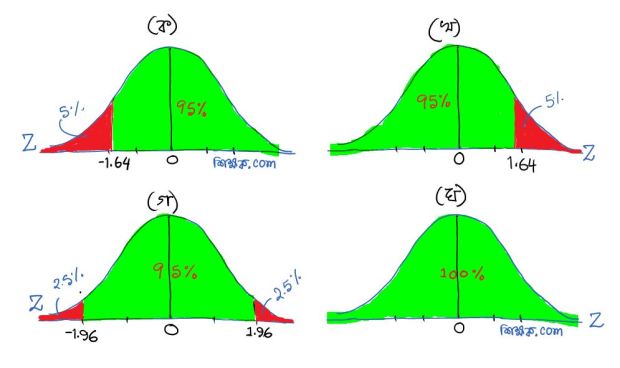
স্মরণ করা যেতে পারে স্ট্যান্ডার্ড নরমাল বিন্যাস দেখতে নিচের চিত্রগুলোর মতো স্তুপাকার।
আগেই দেখেছি কাটঅফ পয়েন্ট নাস্তি প্রকল্পের মানের চেয়ে বেশী, কম, কিংবা ভিন্ন হতে পারে যেটি নির্ভর করে প্রতিপ্রকল্পের উপর। প্রতিপ্রকল্প যদি (ক) হয় (গড় বয়স ২৪ এর কম) তাহলে কাটঅফ পয়েন্ট হবে বিন্যাসের বাম দিকে (চিত্র—ক দ্রষ্টব্য), যদি (খ) হয় (গড় বয়স ২৬ এর বেশী) তাহলে কাটঅফ পয়েন্ট হবে বিন্যাসের ডান দিকে (চিত্র—খ দ্রষ্টব্য), আর যদি (গ) হয় (গড় বয়স ২৪ নয়) তাহলে কাটঅফ পয়েন্ট হবে বিন্যাসের উভয় দিকে (চিত্র—গ দ্রষ্টব্য).
উপরের চিত্রগুলিতে কাটঅফ পয়েন্ট নির্ধারণ করা হয়েছে এমনভাবে যেন সিদ্ধান্তগ্রহণে ভুলের মাত্র ৫% এর বেশী না হয়। (ক), (খ), (গ) — চিত্রে সবুজ এবং লাল দুটি অংশ আমরা দেখতে পাচ্ছি। আনুভূমিক রেখাটি (x-axis) টেস্ট স্ট্যাটিসটিক বা জেড এর মান নির্দেশ করছে। লাল অংশটুকুকে পরিসংখ্যানের ভাষায় বাতিল এলাকা (Rejection region) বলে। আর সবুজ অংশটুকুকে গ্রহণ-এলাকা (Non-rejection region) বলে। অর্থাৎ টেস্ট স্ট্যাটিসটিকের মান যদি বাতিল একায় পড়ে তাহলে আমরা নাস্তি প্রকল্পকে বাতিল করার পক্ষে মত দিতে পারবো, আর যদি সবুজ এলাকা বা গ্রহণ-এলাকায় পড়ে তাহলে বাতিল করার পক্ষে মত দিতে পারবো না।
এই কাটঅফ পয়েন্ট গুলো নির্ধারিত হয় কতটুকু আস্থাশীল ফল চান তার উপর। সাধারণত সিদ্ধান্তগ্রহণে ৫% পর্যন্ত ভুল সহ্য করা হয়। আপনার ভুলের সহনীয়তার মাত্রা পরিবর্তিত হলে কাটঅফ পয়েন্টগুলোও পরিবর্তন করতে হবে। স্ট্যান্ডার্ড নরমাল বিন্যাসের সারণি থেকে সহজেই আমরা এই পয়েন্টগুলো বের করতে পারি।
(ক) এবং (খ) চিত্রে বাতিল এলাকা গুলো বিন্যাসের একপাশে (একেবারে ডান দিকে অথবা একেবারে বাম দিকে) অবস্থান করছে। কিন্তু (গ) চিত্রে বাতিল এলাকাগুলো বিন্যাসের দুই পাশেই অবস্থান করছে। এর কারণ হলো প্রতি-প্রকল্প (গ)-তে আমরা বলেছিলাম জনগোষ্ঠির গড় বয়স ২৪ নয়। যার অর্থ দাঁড়ায় ২৪ বছরের চেয়ে বেশী কিংবা ২৪ বছরের চেয়ে কম। সেজন্যই বাতিল এলাকাগুলো বিন্যাসের দুইপাশে হয়েছে। লক্ষ্য করুন, এক্ষেত্রে বাতিল এলাকাদুটিকে বিন্যাসের দুই পাশে সমান দুই ভাগে ভাগ করে দেয়া হয়েছে। প্রতিটি ভাগে ২.৫% করে মোট ৫%. একারণেই (গ)-তে কাটঅফ পয়েন্টও (ক) ও (খ) –এর চেয়ে আলাদা।
এবারে আসুন উদাহরণ ২ এর সমস্যাটি সমাধান করি।
উদাহরণ ২ (জনগোষ্ঠির গড় নিয়ে দাবী)
ধরি আমাদের হাইপোথিসিস বা প্রকল্পটি এরকম: শিক্ষক ডট কমে যারা সাইন-আপ করেছেন তাদের গড় বয়স ২৪ বছর। এখানে শিক্ষক ডট কমে সাইন-আপ করা সকলেকে নিয়েই আমাদের জনগোষ্ঠি। ধরি, আমাদের জানা আছে যে এই জনগোষ্ঠিতে শিক্ষার্থীদের বয়সের পরিমিত ব্যবধান (Standard deviation) ৪ বছর। প্রকল্পটি যাচাই করা জন্য ৫০ জন শিক্ষার্থীকে দৈব চয়নের মাধ্যমে নির্বাচিত করে তাদের বয়সের গড় পেয়েছি ২৬. অর্থাৎ নমুনা গড় বা স্যাম্পল মিন = ২৬। ৫% ভুলের মাত্রা ধরে যাচাই করতে চাই যে প্রকৃতপক্ষে গড় বয়স
(ক) ২৪ বছরের চেয়ে কম
(খ) ২৪ বছরের বেশী
(গ) দাবিটি ভুল (অর্থাৎ বয়সের প্রকৃত গড় ২৪ নয়, অন্য)
সমাধান
কুইজ
ধরুন আপনি উপরে উল্লিখত জনগোষ্ঠি থেকে নমুনা জরিপ করে ৩০ জন শিক্ষার্থীকে নির্বাচিত করলেন। সেই নমুনা থেকে গড় বয়স পেলেন ২২ বছর। জনগোষ্ঠিরতে বয়সের পরিমিত ব্যবধান যদি ৪ হয় তাহলে আপনার প্রকল্পটি যে ভুল তা ৫% ভুলের মাত্রা ধরে যাচাই করুন।
উত্তরে তিনটি জিনিস মন্তব্যের মাধ্যমে জানান:
১) নাস্তিপ্রকল্প ও প্রতিপ্রকল্প
২) টেস্ট স্ট্যাটিসটিকের মান
২) সিদ্ধান্ত (প্রকল্পটি বাতিল করলেন নাকি বাতিল করতে পারলেন না)
এর মাধ্যমেই শেষ করে হয়ে গেল পরিসংখ্যান পরিচিতি কোর্সটি। ভবিষ্যতে আবারো নতুন কোন কোর্স নিয়ে আপনাদের কাছে ফিরে আসবো বলে আশা করি।
সবাইকে সাথে থাকার জন্য এবং মাঝে মাঝে ইমেইল করার জন্য অশেষ ধন্যবাদ ও কৃতজ্ঞতা জানাচ্ছি।
ভালো থাকুন।
পুনশ্চ:
এই লেকচারের ক্রমিক নং ১৮. আঠার বছর বয়স হলে আমাদের দেশের মানুষকে পরিণত ধরে নেয়া হয়। আশা করবো ১৮টি লেকচার মনোযোগ দিয়ে পড়লে আপনার পরিসংখ্যান জ্ঞানও পরিণত হয়ে উঠবে।
আগের লেকচার-এর লিংক
লেকচার ২ – গবেষণা পদ্ধতি ও চলক সম্পর্কে ধারণা
লেকচার ৩ – ড্যাটা সামারি বা উপাত্ত সারাংশ (কোয়ালিটেটিভ ভ্যারিয়েবল)
লেকচার ৪ – হিস্টোগ্রাম ও ড্যাটার শেইপ
লেকচার ৫ – কেন্দ্রীয় প্রবণতা ও তার পরিমাপসমূহ
লেকচার ৬ – ভেদ ও এর পরিমাপসমূহ
লেকচার ৭ – তুলনামূলক অবস্থান ও z-score
লেকচার ১১ – কতিপয় জটিল ঘটনার সম্ভাবনা
লেকচার ১২ – দৈব চলক ও তার সম্ভাবনা বিন্যাস